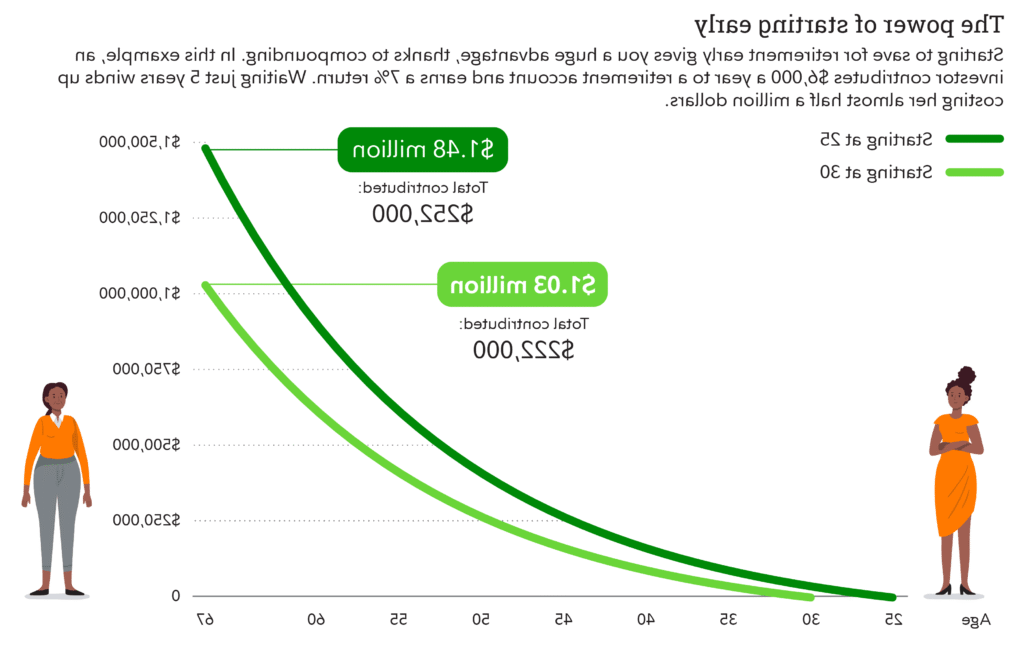
✅ Les intérêts composés font fructifier votre capital en réinvestissant les gains, générant ainsi des profits exponentiels sur le long terme.
Les intérêts composés représentent un mécanisme financier où les intérêts générés par un capital initial sont réinvestis pour produire à leur tour des intérêts. En d’autres termes, c’est l’accumulation des intérêts sur le montant initial plus les intérêts déjà acquis. Ce système permet à un investissement ou à une dette de croître de manière exponentielle au fil du temps, car chaque période d’intérêt inclut à la fois le capital et les intérêts précédemment accumulés.
Nous allons expliquer en détail le fonctionnement des intérêts composés. Nous aborderons les principes de base, la formule mathématique utilisée pour les calculer, et illustrerons avec des exemples concrets comment ils influencent la croissance d’un investissement ou d’une dette. Nous verrons aussi l’importance de la fréquence de capitalisation (annuelle, semestrielle, trimestrielle, mensuelle) et comment elle affecte le rendement total. Enfin, nous donnerons des conseils pratiques pour tirer parti des intérêts composés dans votre gestion financière personnelle ou vos investissements.
Principe des intérêts composés
Contrairement aux intérêts simples qui sont calculés uniquement sur le capital initial, les intérêts composés s’appliquent sur la somme du capital plus les intérêts précédents. Cette technique permet un effet boule de neige où la richesse peut croître rapidement, surtout sur de longues périodes.
La formule des intérêts composés
La formule pour calculer le montant accumulé avec intérêts composés est la suivante :
A = P (1 + r/n)^(nt)
- A : capital final accumulé (capital + intérêts)
- P : capital initial
- r : taux d’intérêt annuel (en décimal)
- n : nombre de périodes de capitalisation par an
- t : durée de l’investissement en années
Exemple concret
Supposons que vous investissiez 1 000 € à un taux annuel de 5 % capitalisé annuellement pendant 10 ans :
- P = 1 000 €
- r = 0,05
- n = 1
- t = 10
Le calcul sera :
A = 1000 × (1 + 0,05/1)^(1×10) = 1000 × (1,05)^10 ≈ 1 628,89 €
Vous aurez donc gagné environ 628,89 € d’intérêts composés en 10 ans.
L’importance de la fréquence de capitalisation
Plus la fréquence de capitalisation est élevée (par exemple mensuelle plutôt qu’annuelle), plus le montant final sera élevé. En effet, les intérêts sont calculés et réinjectés plus souvent dans le capital.
Conclusion partielle
Le mécanisme des intérêts composés est un outil puissant pour faire fructifier votre argent sur le long terme, que ce soit pour un investissement, une épargne ou même pour comprendre le coût d’un emprunt. Une bonne compréhension de ce principe vous aidera à mieux planifier vos finances.
Comment les intérêts composés influencent la croissance de l’épargne
Les intérêts composés jouent un rôle fondamental dans la croissance de l’épargne en permettant à vos gains de générer eux-mêmes des revenus au fil du temps. Contrairement aux intérêts simples, où les intérêts sont calculés uniquement sur le capital initial, les intérêts composés s’appliquent sur la somme totale, c’est-à-dire le capital initial plus les intérêts accumulés précédemment.
Le mécanisme des intérêts composés
Pour bien comprendre leur impact, imaginez la situation suivante :
- Vous déposez 1 000 € sur un compte d’épargne à un taux d’intérêt annuel de 5%.
- Au bout d’un an, vous gagnez 50 € d’intérêts (5% de 1 000 €).
- Au deuxième année, les intérêts s’appliquent non seulement sur 1 000 €, mais aussi sur les 50 € d’intérêts gagnés l’année précédente, ce qui donne 52,50 € d’intérêts.
Ce phénomène crée un effet boule de neige, où vos intérêts génèrent à leur tour des intérêts, accélérant ainsi la hausse de votre épargne.
Exemple pratique : comparaison avec intérêts simples
| Années | Capital avec intérêts simples (5%) | Capital avec intérêts composés (5%) |
|---|---|---|
| 1 | 1 050 € | 1 050 € |
| 5 | 1 250 € | 1 276 € |
| 10 | 1 500 € | 1 629 € |
| 20 | 2 000 € | 2 653 € |
Comme on peut le constater, la différence devient de plus en plus importante avec le temps. Cette illustration démontre à quel point la patience et la durée sont des alliées précieuses pour votre épargne.
Cas d’utilisation concrets
- Plan d’épargne retraite : en commençant tôt, vous bénéficiez pleinement de l’effet des intérêts composés sur plusieurs décennies.
- Investissements en bourse : les dividendes réinvestis qui génèrent de nouveaux dividendes permettent de maximiser la croissance du capital.
- Comptes d’épargne à intérêts composés : offrant des taux d’intérêt plus avantageux que les comptes standards, particulièrement lorsqu’ils capitalisent fréquemment (mensuellement ou trimestriellement).
Conseils pratiques pour maximiser la croissance de votre épargne
- Commencez à épargner le plus tôt possible : chaque année compte pour faire fructifier votre capital.
- Laissez vos intérêts se capitaliser : évitez de retirer vos gains si votre objectif est la croissance à long terme.
- Privilégiez des comptes à capitalisation fréquente : plus les intérêts sont ajoutés régulièrement, plus la croissance est rapide.
- Réinvestissez vos dividendes et gains : dans le cadre d’investissements financiers pour exploiter pleinement l’effet d’accumulation.
Questions fréquemment posées
Qu’est-ce que les intérêts composés ?
Les intérêts composés sont des intérêts calculés sur le capital initial ainsi que sur les intérêts déjà accumulés, générant ainsi un effet boule de neige.
Comment les intérêts composés augmentent-ils l’épargne ?
Ils permettent à l’épargne de croître plus rapidement car les gains générés sont réinvestis pour produire eux-mêmes des intérêts.
Quelle est la différence entre intérêt simple et intérêt composé ?
L’intérêt simple est calculé uniquement sur le capital de départ, tandis que l’intérêt composé s’applique aussi sur les intérêts précédemment gagnés.
Quels facteurs influencent la croissance par intérêts composés ?
Le taux d’intérêt, la fréquence de capitalisation et la durée d’investissement sont des facteurs clés.
Pourquoi est-il important de commencer à épargner tôt ?
Plus l’épargne commence tôt, plus le temps permet aux intérêts composés de maximiser la croissance du capital.
| Facteur | Description | Impact sur la croissance |
|---|---|---|
| Taux d’intérêt | Pourcentage annuel rémunérant le capital | Plus il est élevé, plus la croissance est rapide |
| Capital de départ | Montant initial investi | Plus il est important, plus les intérêts composés seront élevés |
| Durée | Temps pendant lequel l’argent reste investi | Plus la durée est longue, plus l’effet est amplifié |
| Fréquence de capitalisation | Fréquence à laquelle les intérêts sont ajoutés au capital | Capitalisation plus fréquente augmente la croissance |
Nous vous invitons à laisser vos commentaires ci-dessous et à consulter d’autres articles sur notre site pour approfondir vos connaissances en finances personnelles et investissement.